Adaboost是著名的ensemble分类算法,具体算法描述见下图1:

上面算法步骤里,有两个关键点:
-
在第$j$步迭代中,每个样本的权重为:
\[\omega_i = \frac{\exp \left( -f(x_i)y_i \right)} {\sum^n_{i'=1}\exp \left( -f(x_{i'})y_{i'} \right)}, \ \ \forall i = 1, \ldots, n\] -
新子分类器$\varphi_j$对应的权重$\theta_j$使用如下方式获得:
\[\theta_j = \frac12 \log \frac{1-R(\varphi_j)}{R(\varphi_j)} \ \ \text{。}\]注:子分类器$\varphi_j$的输出为$1$或$-1$。
下面从可加模型和指数损失的角度来说明为什么样本权重和子分类器权重的计算公式是上面那样的。
记$m \triangleq f_{\theta}(x) y$(其中$y \in \{-1, 1\}$),指数损失如下定义,它也是0/1损失的一种近似(见下图):
\[J_{\text{exp}}(m) = \exp (-m) \ \ \text{。}\]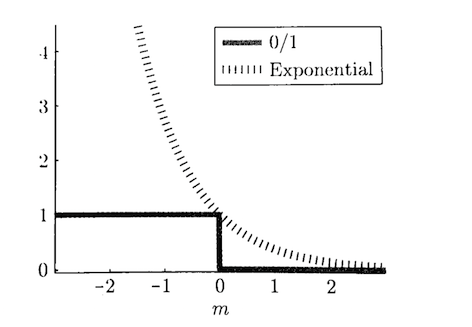
而可加模型是多个输出为$1$和$-1$的二值基函数$\{\varphi_j\}^b_{j=1}$的线性组合:
\[f_{\theta}(x) = \sum_{j=1}^b \theta_j \varphi_j(x) \ \ \text{,}\]它通过最小化指数损失来逐步学习$\varphi_j$:
\[\min_{\theta} \sum_{i=1}^n \exp \left( -f_{\theta}(x_i) y_i \right) \ \ \text{。}\]例如,我们已经获得了$\tilde{f}(x)$,那么学习下一个基函数$\varphi$和$\theta$就是通过最小化下面的指数损失目标函数来获得:
\[\min_{\theta,\ \varphi} \sum_{i=1}^n \exp \left( - \left\{ \tilde{f}(x_i) + \theta \varphi(x_i) \right\} y_i \right) = \min_{\theta,\ \varphi} \sum_{i=1}^n \tilde{\omega}_i \exp \left( - \theta \varphi(x_i) y_i \right) \ \ \text{,}\]其中:
\[\tilde{\omega}_i \triangleq \exp \left( - \tilde{f}(x_i) y_i \right) \ \ \text{。}\]这就是Adaboost里样本权重的计算公式(未归一化)。
不妨设$\theta \geq 0$($\theta < 0$时只要把$\varphi$的符号反一下就行),则:
\[\begin{aligned} &\sum_{i=1}^n \tilde{\omega}_i \exp \left( - \theta \varphi(x_i) y_i \right) \\ &= \exp(-\theta) \sum_{i:\ y_i = \varphi(x_i)} \tilde{\omega}_i + \exp(\theta) \sum_{i:\ y_i \neq \varphi(x_i)} \tilde{\omega}_i \\ &= \left( \exp(\theta)-\exp(-\theta) \right) \sum_{i=1}^n \frac{\tilde{\omega}_i}{2} \left( 1-\varphi(x_i)y_i \right) + \exp(-\theta) \sum_{i=1}^n \tilde{\omega}_i \ \ \text{。} \end{aligned}\]所以,$\varphi$的估计可以通过最小化下面的目标函数获得:
\[\hat{\varphi} = \arg\min_{\varphi} \sum_{i=1}^n \frac{\tilde{\omega}_i}{2} \left( 1-\varphi(x_i)y_i \right) \ \ \text{。}\]而前面的式子对$\theta$求导,并使其等于$0$,可以得到$\theta$的估计:
\[\hat{\theta} = \frac12 \log \frac{1-\hat{R}}{\hat{R}} \ \ \text{,}\]其中
\[\hat{R} \triangleq \frac{1}{\sum_{i=1}^n \tilde{\omega}_i} \sum_{i=1}^n \frac{\tilde{\omega}_i}{2} \left( 1-\varphi(x_i)y_i \right) \ \ \text{。}\]上面计算$\hat{\theta}$的公式,就是Adaboost里子分类器对应权重的计算公式。
经过上面的推导,我们可以认为Adaboost对应着指数损失函数的可加模型。很多研究者也提出了基于其他损失函数的Boosting算法,如MAdaboost和Logitboost等。
更详细的资料可见参考文献1。