特征工程(Feature Engineering)经常被说为机器学习中的black art,这里面包含了很多不可言说的方面。怎么处理好特征,最重要的当然还是对要解决问题的了解。但是,它其实也有很多科学的地方。这篇文章我之所以命名为特征处理(Feature Processing),是因为这里面要介绍的东西只是特征工程中的一小部分。这部分比较基础,比较容易说,所以由此开始。
单个原始特征(或称为变量)通常属于以下几类之一:
- 连续(continuous)特征;
- 无序类别(categorical)特征;
- 有序类别(ordinal)特征。
本文中我主要介绍针对单个特征的处理方法,虽然也会附带介绍基础的特征组合方法。同时处理多个特征,以及更复杂的特征处理方法介绍,以后我再另外细说。下面我由浅入深地逐渐说明针对这三类特征的常用处理方法。
初级篇
这节要讲的处理技术,应该刚接触机器学习不久的同学都会知道。
连续特征
除了归一化(去中心,方差归一),不用做太多特殊处理,可以直接把连续特征扔到模型里使用。
无序特征
可以使用One-hot(也叫One-of-k)的方法把每个无序特征转化为一个数值向量。比如一个无序特征color有三种取值:red,green,blue。那么可以用一个长度为3的向量来表示它,向量中的各个值分别对应于red,green,blue。如:
| color取值 | 向量表示 |
|---|---|
| red | (1, 0, 0) |
| green | (0, 1, 0) |
| blue | (0, 0, 1) |
这种方法在NLP里用的很多,就是所谓的词向量模型。变换后的向量长度对于词典长度,每个词对应于向量中的一个元素。
机器学习书籍里在讲这个的时候介绍的处理方法可能跟我上面说的有点差别。上面说的表达方式里有一个维度是可以省略的。既然我们知道color一定是取3个值中的一个,那么我们知道向量的前两个元素值,就能推断第3个值是多少。所以,其实用下面的方式就可以表达到底是哪种颜色:
| color取值 | 向量表示 |
|---|---|
| red | (1, 0) |
| green | (0, 1) |
| blue | (0, 0) |
这样表达的好处是少用了一个维度,降低了转化后特征之间的相关性。但在实际问题中特征基本都或多或少会有些缺失。使用第一种表达方式就可以用全0的向量来表示值缺失,而第二种表达方式是没法表达缺失的。
有序特征
有些特征虽然也像无序特征那样只取限定的几个值,但是这些值之间有顺序的含义。例如一个人的状态status有三种取值:bad, normal, good,显然bad < normal < good。
当然,对有序特征最简单的处理方式是忽略其中的顺序关系,把它看成无序的,这样我们就可以使用处理无序特征的方式来处理它。在实际问题中,这种处理方式其实用的很多。
当然有些问题里有序可能会很重要,这时候就不应该把其中的顺序关系丢掉。一般的表达方式如下:
| status取值 | 向量表示 |
|---|---|
| bad | (1, 0, 0) |
| normal | (1, 1, 0) |
| good | (1, 1, 1) |
上面这种表达方式很巧妙地利用递进表达了值之间的顺序关系。
中级篇
最容易让人掉以轻心的,往往就是大家觉得最简单的事。在特征处理中,最容易让刚入门同学忽略的,是对连续特征的处理方式。
以线性分类器Linear Regression (LinearReg)为例,它是通过特征的线性加权来预测因变量\(y\):
\[y = w^T x\]但大部分实际情况下,\(y\)与\(x\)都不会是这么简单的线性关系,甚至连单调关系都不会有。举个只有一个特征的例子,如果\(y\)与\(x\)的实际关系如下图:
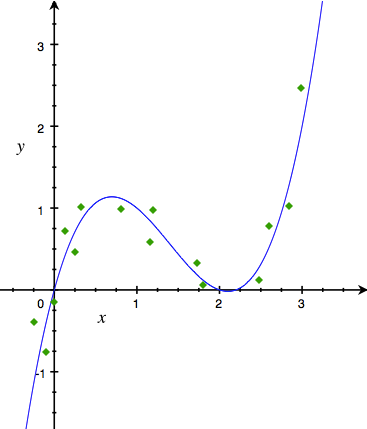
那么直接把\(x\)扔进LinearReg模型是怎么也得不到好结果的。很多人会想着既然线性分类器搞不定,那就直接找个非线性的好了,比如高斯核的SVM。我们确实可以通过这种简单换算法的方式解决这个简单的问题。但对于很多实际问题(如广告点击率预测),往往特征非常多,这时候时间约束通常不允许我们使用很复杂的非线性分类器。这也是为什么算法发展这么多年,广告点击率预测最常用的方法还是Logistic Regression (LogisticReg)。
对于上面这个问题,有没有什么办法使得LinearReg也能处理得不错?当然是有,就是对原始特征\(x\)做转化,把原来的非线性关系转化为线性关系。
方法一:离散化
最常用的转化方式是对\(x\)做离散化(discretization),也就是把原来的值分段,转化成一个取值为0或1的向量。原始值落在某个段里,向量中此段对应的元素就为1,否则为0。
离散化的目标是\(y\)与转化后向量里的每个元素都保持比较好的线性关系。
比如取离散点\(\{0.5, 1.5, 2.5\}\),通过判断\(x\)属于\((-\infty, 0.5)\),\([0.5, 1.5)\),\([1.5, 2.5)\),\([2.5, +\infty)\)中哪段来把它离散化为4维的向量。下面是一些例子的离散结果:
| 原始值\(x\) | 离散化后的值 |
|---|---|
| 0.1 | (1, 0, 0, 0) |
| 1.3 | (0, 1, 0, 0) |
| 3.2 | (0, 0, 0, 1) |
| 5.8 | (0, 0, 0, 1) |
离散化方法的关键是怎么确定分段中的离散点。下面是常用的选取离散点的方法:
- 等距离离散:顾名思义,就是离散点选取等距点。我们上面对\(x\)取离散点\(\{0.5, 1.5, 2.5\}\)就是一种等距离散,见下图。图中垂直的灰线代表离散点。
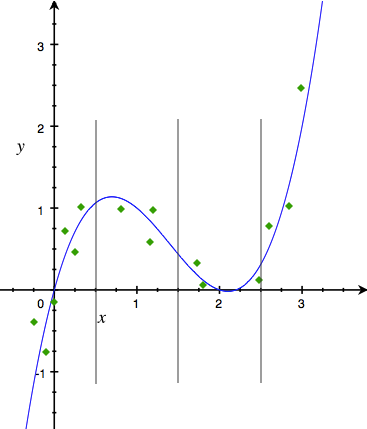
- 等样本点离散:选取的离散点保证落在每段里的样本点数量大致相同,见下图。
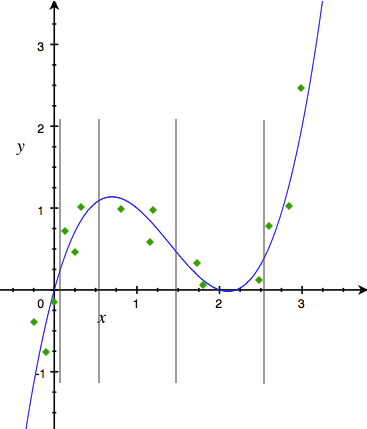
- 画图观察趋势:以\(x\)为横坐标,\(y\)为纵坐标,画图,看曲线的趋势和拐点。通过观察下面的图我们发现可以利用3条直线(红色直线)来逐段近似原来的曲线。把离散点设为两条直线相交的各个点,我们就可以把\(x\)离散化为长度为3的向量。
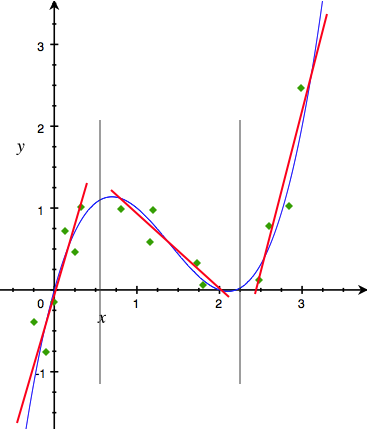
上面介绍的这种离散化为0/1向量的方法有个问题,它在离散时不会考虑到具体的\(x\)到离散边界的距离。比如等距离散中取离散点为\(\{0.5, 1.5, 2.5\}\),那么1.499,1.501和2.49分别会离散为(0, 1, 0, 0),(0, 0, 1, 0)和(0, 0, 1, 0)。1.499和1.501很接近,可是就因为这种强制分段的离散导致它们离散的结果差距很大。
针对上面这种硬离散的一种改进就是使用软离散,也就是在离散时考虑到\(x\)与附近离散点的距离,离散出来的向量元素值可以是0/1之外的其他值。有兴趣的同学可以去ESL1这本书中找点感觉。
方法二:函数变换
函数变换直接把原来的特征通过非线性函数做变换,然后把原来的特征,以及变换后的特征一起加入模型进行训练。常用的变换函数见下表,不过其实你可以尝试任何函数。
| 常用非线性函数\(f(x)\) | \(x\)的取值范围 |
|---|---|
| \(x^\alpha\); \(\alpha \in (-\infty, +\infty)\) | \((-\infty, +\infty)\) |
| \(\log(x)\) | \((0, +\infty)\) |
| \(\log\left(\frac{x}{1-x}\right)\) | \((0, 1)\) |
这个方法操作起来很简单,但记得对新加入的特征做归一化。
对于我们前面的问题,只要把\(x^2\),\(x^3\)也作为特征加入即可,因为实际上\(y\)就是\(x\)的一个三次多项式。
高级篇
笛卡尔乘积
我们可以使用笛卡尔乘积的方式来组合2个或更多个特征。比如有两个类别特征color和light,它们分别可以取值为red,green,blue和on, off。这两个特征各自可以离散化为3维和2维的向量。对它们做笛卡尔乘积转化,就可以组合出长度为6的特征,它们分别对应着原始值对(red, on),(red, off),(green, on),(green, off),(blue, on),(blue, off)。下面的矩阵表达方式更清楚地说明了这种组合。
| X | on |
off |
|---|---|---|
red |
||
green |
||
blue |
对于3个特征的笛卡尔乘积组合,可以表达为立方的形式。更多特征的组合依次类推。 这个方法也可以直接用于连续特征与类别特征之间的组合,只要把连续特征看成是1维的类别特征就好了,这时候组合后特征对应的值就不是0/1了,而是连续特征的取值。
离散化续篇
在上节中我已经介绍了一些常用的离散化单个连续特征的方法,其中一个是画图观察趋势。画图观察趋势的好处是直观、可解释性强,坏处是很麻烦。当要离散化的特征很多时,这种方法可操作性较差。
机器学习中有个很好解释,速度也不错的模型——决策树模型。大白话说决策树模型就是一大堆的if else。它天生就可以对连续特征分段,所以把它用于离散化连续特征合情合理。我称这种方法为决策树离散化方法。例如Gmail在对信件做重要性排序时就使用了决策树离散化方法2。
决策树离散化方法通常也是每次离散化一个连续特征,做法如下:
单独用此特征和目标值\(y\)训练一个决策树模型,然后把训练获得的模型内的特征分割点作为离散化的离散点。
这种方法当然也可以同时离散化多个连续特征,但是操作起来就更复杂了,实际用的不多。
核方法
核方法经常作为线性模型的一种推广出现。以线性回归模型为例,它对应的核方法如下:
\[f_{\theta}(x) = \sum_{i=1}^n \theta_i K(x, x_i) \ \ \text{,}\]其中$\{x_i\}^n_{i=1}$为训练样本点,$K(x_i, x_j)$为核函数,比如常用的高斯核函数为:
\[K(x_i, x_j) = \exp \left( -\frac{\|x_i - x_j\|_2^2}{2 h^2} \right) \ \ \text{。}\]如果我们把上面模型里的$\{K(x, x_i)\}^n_{i=1}$看成特征,而$\theta$看成模型参数的话,上面的模型仍旧是个线性模型。所以可以认为核方法只是特征函数变换的一种方式。
当然,如果把核函数$K(x_i, x_j)$看成一种相似度的话,那上面的模型就是kNN模型了,或者叫做加权平均模型也可以。
因为核方法在预测时也要用到训练样本点,耗内存且计算量大,所以在数据量较大的实际问题中用的并不多。
到此,我已经介绍了不少针对单个特征的处理方法。这些处理方法很难说哪个好哪个不好。有些问题这个好,有些问题那个好,也没什么绝招能直接判断出哪种方法能适合哪些问题。唯一的招就是:
Experiment a lot!
References
-
Trevor Hastie et al. The Elements of Statistical Learning, 2001. ↩
-
Douglas Aberdeen et al. The Learning Behind Gmail Priority Inbox, 2010. ↩