假设我们要求解以下的最小化问题:
\[\min\limits_x f(x) \ \ \text{。}\]如果$f(x)$可导,那么一个简单的方法是使用Gradient Descent (GD)方法,也即使用以下的式子进行迭代求解:
\[x_{k+1} := x_{k} - \alpha \nabla f(x_{k}) \ \ \text{。}\]对GD的一种解释是$x_k$沿着当前目标函数的下降方向走一小段,只要步子足够小,总能保证得到 $f(x_{k+1}) \leq f(x_k)$。
如果$\nabla f(x)$满足L-Lipschitz条件,即:
\[\parallel \nabla f(x') - \nabla f(x) \parallel \leq L \parallel x’ - x\parallel \ \ \text{,}\]那么我们可以在点$x_k$附近把$f(x)$近似为:
\[\hat{f}(x, x_k) \triangleq f(x_k) + \langle \nabla f(x_k), x - x_k \rangle + \frac{L}{2} \parallel x - x_k \parallel_2^2 \ \ \text{。}\]把上面式子中各项重新排列下,可以得到:
\[\begin{aligned} \hat{f}(x, x_k) &\triangleq f(x_k) + \langle \nabla f(x_k), x - x_k \rangle + \frac{L}{2} \parallel x - x_k \parallel_2^2 \\ & = \frac{L}{2} \parallel x - (x_k - \frac1L \nabla f(x_k)) \parallel_2^2 + \varphi(x_k) \ \ \text{。} \end{aligned}\]显然$\hat{f}(x, x_k)$的最小值在
\[x_{k+1} = x_k - \frac 1 L \nabla f(x_k)\]获得。所以,从这个角度上看的话,GD的每次迭代是在最小化原目标的一个二次近似函数。
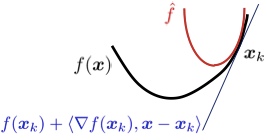
在很多最小化问题中,我们往往会加入非光滑的惩罚项$g(x)$,比如常见的L1惩罚:$g(x) = \parallel x \parallel_1$。这个时候,GD就不好直接推广了。但上面的二次近似思想却可以推广到这种情况:
\[\begin{aligned} x_{k+1} &= \arg \min\limits_x \hat{F}(x, x_k) \\ &= \arg \min\limits_x \frac{L}{2} \parallel x - (x_k - \frac1L \nabla f(x_k)) \parallel_2^2 + g(x) \ \ \text{。}\end{aligned}\]这就是所谓的Proximal Gradient Descent(PGD)算法1。只要给定$g(x)$时下面的最小化问题能容易地求解,PGD就能高效地使用:
\[\text{prox}_{\mu g}(z) = \arg \min\limits_x \frac12 \parallel x - z \parallel_2^2 + \mu g(x) \ \ \text{。}\]比如$g(x) = \parallel x \parallel_1$时,$\text{prox}_{\mu g} (z)$能够通过所谓的soft thresholding获得:
\[\text{prox}_{\mu g} (z) = \text{sign}(z) \max\{\mid z \mid - \mu, \ 0\} \ \ \text{。}\]References
-
John Wright. Lecture III: Algorithms, 2013. ↩